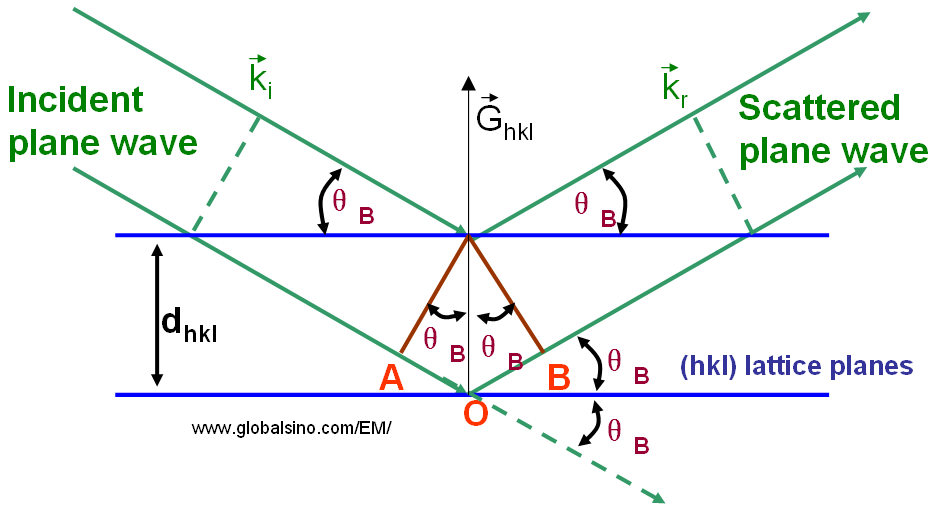
Facendo incidere un'opportuna onda elettromagnetica su di un cristallo si osservano fenomeni di interferenza, causati dalla riflessione di onde da parte di piani cristallini diversi ma paralleli. Questo fenomeno fu interpretato per la prima volta da William Henry Bragg e suo figlio William Lawrence Bragg nel 1913 e riassunto nella cosiddetta legge di Bragg:
dove:
- (theta) è l'angolo che il fascio uscente forma col piano cristallino
- (lambda) è la lunghezza d'onda della radiazione
- è la distanza tra due piani adiacenti
- è un intero positivo.
La formula si spiega in maniera analitica considerando una differenza di cammino ottico pari a .
La legge di Bragg può essere interpretata geometricamente nello spazio reciproco come sfera di Ewald.
Tracciando un grafico che abbia come ascisse i valori della frequenza di radiazione e come ordinate i valori della quantità di moto si ottiene che quest'ultima dipende linearmente dalla lunghezza d'onda in maniera inversamente proporzionale, e che il prodotto tra le due è una costante che misurata vale esattamente la costante di Planck. Si deduce che ad ogni particella in moto è associata una lunghezza d'onda, il che è un passo fondamentale per la formulazione del Dualismo onda-particella formulato da De Broglie.
Note
Voci correlate
- Condizione di von Laue
- Reticolo di Bragg
- Diffrazione dei raggi X
Altri progetti
- Wikimedia Commons contiene immagini o altri file su legge di Bragg
Collegamenti esterni
- (EN) Legge di Bragg, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.